The Tithonus Option is Not an Option
Anti-ageing technology may present us with the awful scenario of extended lifespan but limited improvement in quality of life. Living forever -- or at least for long periods of time -- with dementia is known as "The Tithonus Option." This paper argues that the Tithonus Option is unlikely to eventuate. Copyright © Chris Lawson
[0] Introduction
Summary
Anti-ageing technology may present us with the awful scenario of extended lifespan but limited improvement in quality of life. Living forever -- or at least for long periods of time -- with dementia is known as "The Tithonus Option."
This paper argues that the Tithonus Option is unlikely to eventuate. [This paper was presented at the Worldcon SF Convention, Melbourne Australia on 6 September 1999. Many thanks to Damien Broderick, who started my brain working on the subject, to Russell and Jenny Blackford, who were instrumental in developing the academic track at the Worldcon, and most of all to the audience whose questions and comments helped clarify and extend the presentation you see here.]
The Future of Ageing
Future technology offers us visions of power that rival the dreams of myth and legend. As Clarke's Law puts it: "any sufficiently advanced technology is indistinguishable from magic." One of those magic dreams is of immortality. However, as in the legends, immortality comes at a price.
In this paper I have not addressed population control or equitable distribution of anti-ageing technology, although I do not mean to dismiss their importance. This paper addresses another possibility altogether: the fear that we will live longer, but in bad health and decrepitude.
This is the "Tithonus Option" -- immortal life with eternal dementia. I will be arguing that the Tithonus Option is not a strong possibility even in the advent of advanced anti-ageing technology.
[This article germinated when Damien Broderick asked me to look over some chapters of his book on immortality, The Last Mortal Generation. The "Tithonus Option" piqued my interest and I replied to Damien with a short version of the argument on these pages. You can find that summary in Damien's book.]
Tithonus and Eos
In Greek mythology, Tithonus was a handsome mortal who fell in love with Eos, the goddess of the dawn. Eos realised that her beloved Tithonus was destined to age and die. She begged Zeus to grant her lover immortal life.
Zeus was a jealous god, prone to acts of deception in order to seduce beautiful gods and mortals, and he was not pleased with Eos's infatuation with a rival. In a classic Devil's Bargain, he granted Eos's wish -- literally. He made Tithonus immortal, but did not grant him eternal youth.
As Tithonus aged, he became increasingly debilitated and demented, eventually driving Eos to distraction with his constant babbling.
In despair, she turned Tithonus into a grasshopper. In Greek mythology, the grasshopper is immortal. (In a close cultural parallel, the Chinese believed that locusts live forever.) This myth also explains why grasshoppers chirrup ceaselessly, like demented old men.
[1] Modern Tithonus Myths
Summary
There are several foreseeable outcomes for anti-ageing technology. Various scenarios arise in science fiction stories such as R.G. Riel's "A Short Prayer" and Ian McDonald's "The Days of Solomon Gursky."
We live in a special period of history. For the first time, the majority of people living in the First World can expect to live well into their seventies. Even so, our final years are usually marked by impaired health and often senile dementia. However, new technologies have the potential to extend our lifespan, perhaps indefinitely. I am talking here of advances in genetic engineering and the blue-sky future of nanotechnology.
There are three foreseeable futures. The first is that we will live and die much as we do today. It is almost inevitable that genetics will provide new ways of extending our lives, but there is no guarantee that these life extensions will add more than a few years or significantly reduce the prevalence of dementia and debility. The second possibility is that technology will grant large extensions in lifespan, but will not be able to stave off dementia. This is the Tithonus Option. The third possibility is that technology will be able to repair the damage done to our cancer cells and arteries and neurons, thus giving us effective immortality.
A Modern Tithonus Myth
In R.G. Riel's "A Short Prayer" (Eidolon #22/23), a priest is kept alive for centuries on life support. As his body decays, ever more invasive procedures are performed to save him, and more and more of his vital bodily functions are taken over by machines. Eventually all that is left of the original priest is a small part of his brain which recites catechisms over and over.
This is the nightmare of the Tithonus Option: Eternal life, or at least centuries-long life, with zero quality of life.
Superficially, this seems a reasonable possibility. While genetic engineering and nanotechnology may help extend our lives for centuries, it does not follow that future technology will be able to repair all wear-and-tear on the brain and heart. Unless future technology can repair all microscopic injuries, then the Tithonus Option ought to be a possibility.
I will be arguing, however, that the Tithonus Option is not a likely outcome -- but for other reasons.
A Modern Immortality Myth
Ian McDonald's novella "The Days of Solomon Gursky" (Asimov's SF, June 1998) follows the life of a nanotech designer whose inventions allow humans to stave off disease and improve their bodies. They are effectively immortal barring extreme accidents such as nuclear explosions.
Solomon Gursky manages to travel the limits of the cosmos and eventually outlives the Universe itself.
This is immortality, or the Gursky Option. Gurskys can live forever, and in excellent health.Only accidents, murders, and suicides can kill Gurskys since virtually all human disease is curable.As we shall see, Gurskys' lifespans are measured not by life expectancy but by half-life.
[2] Exponential and Gurskian Death Rates
Summary
Currently, death rates increase exponentially with age (approximately). It is feared that anti-ageing technology will prolong life, but will not prevent dementia or other causes of increasing debility. Immortals such as Solomon Gursky have access to such powerful medical technology that they only die from accident, murder, or suicide. Gursky lifespans are best measured by half-lives.
Australian data shows an approximately exponential increase in death rate by age. Although one would expect regional and sociocultural differences, the broad picture should apply equally well in any Western nation.
Death rates are expressed as deaths per 100,000 people per year.
The Tithonus Option is the Middle Path
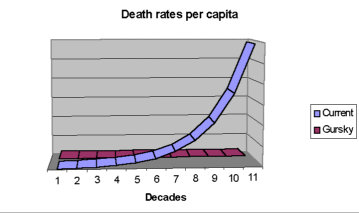 Data collected by the Australian Bureau of Statistics (ABS) shows an exponential increase in deaths per year when separated into age groups.
Data collected by the Australian Bureau of Statistics (ABS) shows an exponential increase in deaths per year when separated into age groups.
[The ABS data is tabulated in an odd fashion. The age brackets are: less than 1 year, 1-14, 15-24, 25-44, 45-54, 55-64, 65-74, 75-84, and 85 and over.]
By comparison, Gurskys have a constant death rate per annum. They experience no increase in death rate with age.
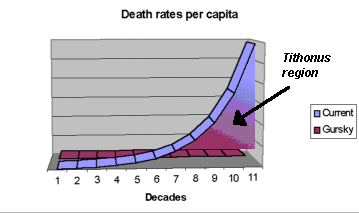
The Tithonus Option lies in the area between these two curves. With the current pattern of death rate, most people will die within a few years of developing dementia or severely reduced mobility. Gurskys, with their access to highly advanced medical technology, would not expect their health to deteriorate over time.
Therefore longevity plus debility lies somewhere between the Gurskys and modern mortals.
Population Curves
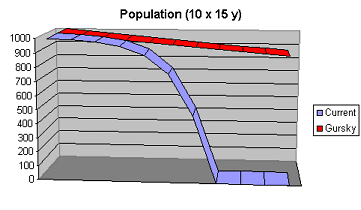 A population curve is a graph of the number of surviving members of a cohort plotted against age. These curves are the same as the cumulative death rate subtracted from a set population. [These curves are approximately the same as the death rate curves above flipped on the y-axis.]
A population curve is a graph of the number of surviving members of a cohort plotted against age. These curves are the same as the cumulative death rate subtracted from a set population. [These curves are approximately the same as the death rate curves above flipped on the y-axis.]
The graph above shows the exponential death rate increasing to form a population crash in the later decades. The Gursky population, with its non-exponential death rate, shows a steady population attrition but no population crash. Only a small fraction of the Gurskys have died by the time the entire cohort of today is gone.
Gurskys Have Half-Lives
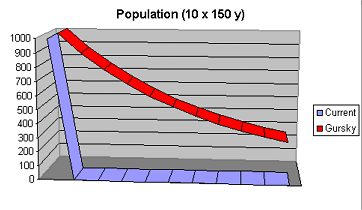 The scale on the graph above hides some valuable information. When the x-axis is scaled up by a factor of ten (that is, each block on the x-axis represents 150 years instead of 15 years, see right), the population curve of Gurskys reveals a steady decay curve just like the decay of radioactive elements.
The scale on the graph above hides some valuable information. When the x-axis is scaled up by a factor of ten (that is, each block on the x-axis represents 150 years instead of 15 years, see right), the population curve of Gurskys reveals a steady decay curve just like the decay of radioactive elements.
Just as for radioactive elements, Gursky populations are best measured by half-life rather than by life expectancy.
This has several important ramifications. There is no upper limit on the age of a Gursky.Based on modern calculations, a population that only dies in accidents will have a half-life of500 years. [This assumes that the rate of fatal accidents will remain constant despiteimproved medical technology and that there will be minimal psycho-social changes with the availability of virtual immortality. These assumptions are unlikely to hold true, but it is the best approximation we can make today.]
Note that a Gursky who has lived 500 years has a 50% chance of living another 500 years. And should a Gursky survive that to reach 1000 years of age, he still has a 50% chance of living another 500 years. This is always true: no matter what the age of a Gursky, he has a 50% chance of surviving another half-life.
As the curve makes clear, modern mortals are a mere blip in the lives of Gurskys.
[3] The Reason for Exponential Death Rates
Summary
Death rate increases exponentially because our bodies accumulate damage.Errors in our DNA lead to cancer. Plaques accumulate in our arteries and cause strokeand heart disease. Diseases of "accumulated damage" exhibit exponential growth curves.Some causes of death can only be modelled approximately by an exponential curve (accidents), others bear no relationship (murder and suicide).
Accumulated Mutation Load is Exponential
The graph below plots the rate of death from colon cancer by age. It shows an exponential growth curve.
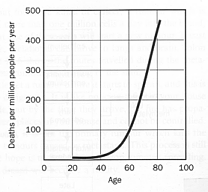 Cancer is not a simple disease. It results when a cell begins to reproduce uncontrollably.Since our cells contain several safety mechanisms, a cancer cell has to bypass many safety nets in order to survive. This means that each cell has to accumulate several mutations or it will not become a clinical cancer. In the case of colon cancer, six separate mutations are necessary to convert a normal colonic cell into a malignant tumour.
Cancer is not a simple disease. It results when a cell begins to reproduce uncontrollably.Since our cells contain several safety mechanisms, a cancer cell has to bypass many safety nets in order to survive. This means that each cell has to accumulate several mutations or it will not become a clinical cancer. In the case of colon cancer, six separate mutations are necessary to convert a normal colonic cell into a malignant tumour.
This explains why cancer deaths exhibit an exponential curve: it takes years of accumulated mutations for cells to begin turning malignant. Also, the rate of mutation itself also increases over time as our bodies accumulate a greater load of radiation and chemical mutagens. So it is no surprise that cancer increases exponentially with age.
Cancer
Cancer is caused by accumulated mutational load over time.Most primary cancers are not fatal in themselves unless they cause direct damage to vital body parts, such as a brain tumour compressing the contents of the skull.
Instead, most fatal cancers are the result of secondary tumours that have spread throughout the body via blood or lymphatics. The most common sites of secondary tumours are the lungs, liver, and brain.
Vascular Disease
While cancers are the result of accumulated errors in DNA, vascular disease is the result of accumulated errors in arteries called atheroma or plaque. Atheromas are flash points for clots, which can then break off and become lodged in a narrowing of an artery, blocking off the blood supply to the tissues supplied by that artery.
A massive heart attack can cut off the blood supply to the bottom of the heart. Having no blood supply, this part of the heart dies, with the result that the heart then fails to act as an efficient pump -- and then the rest of the body is in serious peril. Surrounding the heart is a blood clot that formed when blood leaked through the damaged heart wall to form a capsular clot around the heart.
Strokes most commonly arise from the same pathological mechanism as a heart attack. That is, a clot breaks off from an arterial plaque. The clot then lodges in one of the small arteries in the brain, cutting off the blood supply and killing brain tissue.
Consider instead a haemorrhagic stroke -- it is caused by an artery bursting in the brain and the blood pouring out under pressure. The resulting blood clot kills brain tissue by direct pressure effect. Although this is a different mechanism to the "occlusive" strokes mentioned above, it is caused by long-standing hypertension (high blood pressure) wearing down the elasticity of arterial walls. As such, it represents another example of accumulated errors, and therefore follows an exponential curve when plotted against age.
Accidents
Accidental deaths follow a complex curve. Young people are more likely to die of accidents thanthose in their forties. This is due to the high rate of risk-taking behaviours. Young peopleare more likely to drive faster or ski a dangerous slope, for instance. With increasing age comes increasing safety awareness. So the curve for accidental death shows a distinct "hill" with a peak in the late teens/early twenties.
However, after that blip due to risk-taking, accidents reassert an exponential curve. The elderly are far more likely to die as a result of accidents than even the highest risk-taking age group. We tend to neglect this problem because accidental deaths in the elderly are significantly fewer than deaths by vascular disease or cancer, whereas in young people accidents are the most common cause of all deaths.
Accidental deaths show an exponential curve because, in the elderly, they too are the result of accumulated damage. Reduced balance, co-ordination, and reflex response times put the elderly at greater risk of having an accident. Osteoporosis means that smaller forces can result in significant injuries. Diabetes and vascular disease mean that injuries take longer to heal, thus increasing the risk of immobility and infirmity. As a result, accidental deaths can be roughly modelled by an exponential curve.
Homicide and Suicide
Murder and suicide do not follow an exponential growth curve because they are not caused byaccumulated bodily errors. The causes of murder and suicide are extremely complex, and dependon social, cultural, and psychological factors, none of which are amenable to simple formulaicanalysis.
Since the death rate from murder and suicide in most societies is dwarfed by other causes, we shall ignore it for the purpose of this argument. However, it is worth noting that prolonged lifespans may result in increasing suicide rates and risk-taking if boredom sets in. It is very difficult to predict the death-rate profile of future societies.
Exponential Curves and the Western Way of Dying
In non-Western societies, especially those where life expectancy is still hovering around the mid-forties, cancer and vascular disease are relatively uncommon causes of death. Infection and malnutrition are still the primary causes of death in Third World countries.
This has interesting implications for Westerners. As our medical technology and public healthstrategies improve, we have eradicated infection and malnutrition as the major causes of death.(People still die of infections and nutritional deficiencies, but these are no longer in the same ballpark as cancer or heart disease.)
I would argue that diseases of accumulated damage, that is those that exhibit an exponentialgrowth curve, are destined to be the primary causes of death in wealthy countries. With wealth,nations can reduce the rate of infections, but even applied efforts to reduce heart disease orrisk of cancer are limited by the exponential nature of their progress. Even if we can reducethe incidence of heart attacks by, say, 50% at the age of 65, this will only prolong lifespan by a few years because the exponential curve will quickly catch up.
The only possible escape from these cumulative diseases is if we develop advanced medical technology capable of repairing our bodily errors. This is the Gursky Option.
[4] Excluding Causes of Death Does Not Dramatically Extend Lifespan
Summary
Excluding selected causes of death (such as cancer) makes very little difference to life expectancy in an exponential scenario. Even a ten-fold reduction in base death rate leads to less than a doubling of life expectancy. Exponential death rates necessarily put severe limits on the possibility of longevity beyond two centuries.
Death Rates in Australia
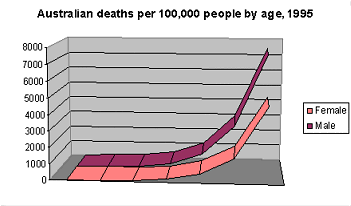
The graph above shows the death rate in Australia plotted against age. As it shows, the curve is roughly exponential and males have a more dramatic increase than females.
Roughly speaking, the curve for males can be decribed as death rate = 1.118 age and for females as death rate = 1.111 age, where age is in years and death rate is in deaths per 100,000 people per year.
This is, I must point out, an approximation. The death curves do not follow perfect exponential functions. Death curves are best seen as a sum of many curves from specific causes of death, some with slightly different values of the constant (that is, the a in the function y = a x), and some which are not exponential at all.
Real and Idealised Death Rates
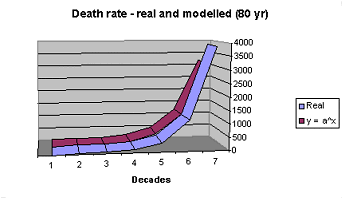 As the graph to the right shows, the real death curve as drawn from ABS data on death rates is a close match to an exponential curve. There are slight differences between the two curves, but clearly an exponential function is a reasonable approximation of real death rates.
As the graph to the right shows, the real death curve as drawn from ABS data on death rates is a close match to an exponential curve. There are slight differences between the two curves, but clearly an exponential function is a reasonable approximation of real death rates.
When male and female deaths are combined, the function that best fits the curve is:death rate = 1.114 age, where age is in years and death rate is expressed asdeaths per 100,000 people per year.
 When one draws the curve out past the limit of ABS statistics (see right), one sees the sharp upsweep of the death rate curve on the idealised exponential function. (The ABS data runs out at "greater than 85 years.") Note that these curves are exactly the same as in the graph above, only on a greater scale and with the idealised curve projected past the domain limit of the real curve.
When one draws the curve out past the limit of ABS statistics (see right), one sees the sharp upsweep of the death rate curve on the idealised exponential function. (The ABS data runs out at "greater than 85 years.") Note that these curves are exactly the same as in the graph above, only on a greater scale and with the idealised curve projected past the domain limit of the real curve.
While it is difficult to draw a life expectancy from these curves, one can derive a "life limit", that is, the greatest age one would expect a person to reach. This limit can be derived by extrapolating the exponential curve until the death rate per 100,000 people per year is greater than 100,000. Clearly, at this point one would expect all humans at the life limit to die within the year. [Note that this is a statistical point; there is no absolute requirement for every single person of that age to die in that year.]
By this exponential curve, the life limit for males is 103.2 years, and for females is 109.4 years. [
The Surprising Stability of Life Limit
Originally I had planned to respond to Damien Broderick about the terrible possibility of the Tithonus Option. I took the original ABS data on death rates and excluded causes that I believed would be most likely to be cured by future genetic technology.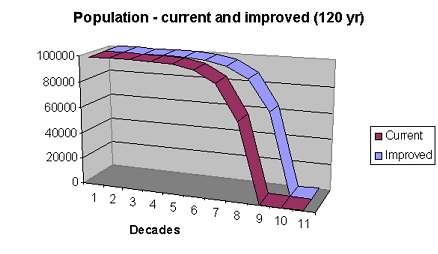 I excluded: infection, cancer, congenital anomalies, pregnancy-related deaths, immune disease, haematological conditions, endocrine conditions, and dermatological conditions. Then I recalculated the exponential function to be y = 1.105 age, which yieldeda life limit of 115, a mere 9 years better than the current life limit!
I excluded: infection, cancer, congenital anomalies, pregnancy-related deaths, immune disease, haematological conditions, endocrine conditions, and dermatological conditions. Then I recalculated the exponential function to be y = 1.105 age, which yieldeda life limit of 115, a mere 9 years better than the current life limit!
The graph compares the current population curve with the population curve with the excluded diseases. As this makes clear, even excluding important disease groups such as cancer (which results in roughly 30% of all deaths) makes only minimal changes to the life limit.
This finding surprised me since I had expected a far greater extension in lifespan.To confirm my new suspicions, I postulated extremely effective medical technology and came up with the graph to the right. These curves were derived by taking the death rate of females aged 70, excluding the causes mentioned above, and dividing by two. This gave a "fantasy" function of deaths = 1.089 age. Remarkably, this function yielded a life limit of 135.0 years, a tiny increase given the halving of the death rate at age 70.
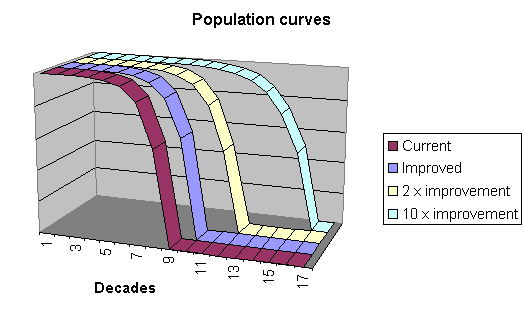
To push the concept even further, I postulated an "extreme fantasy" scenario in which the death rate of idealised women aged 70 was only a tenth its current value. [That is, only 80 deaths per 100,000 people per year compared to 798 as derived from the ABS statistics with the above conditions excluded.] This yielded the function deaths = 1.065 age, with a modest increase in life limit to 183.9 years. This means that reducing the current death rate by more than a factor of ten leads to less than a doubling of life limit.
Even more remarkable is the slope of the population curves. Clearly, even in the "extreme fantasy" (10x improvement) scenario, the population curve plunges dramatically. This means that there is little difference on the Tithonus region of the "extreme fantasy" curve compared to that of the current curve. In short, even dramatic improvements in medical technology will not result in the Tithonus Option.
[5] Conclusion
Summary
Exponential death rates and increasing debility go hand in hand. Solve one and the other must follow (Gurskian immortality). If debility persists, then so will exponential death (current pattern). Therefore the Tithonus Option is not a likely outcome of anti-ageing technology.

This graph is repeated from the end of the last page because it shows the core of the argument. Even when death rates are slashed dramatically for the purpose of modelling advanced medical technology, the death rates increase exponentially, the population curve crashes, and there is still virtually no window for the Tithonus Option.
The Tithonus Option exists in a region that will never be dramatically enlarged by medical intervention. If future technology can repair the errors that accumulate in our bodies, then we will not become demented or debilitated and we will have become Gurskian immortals. If our future technology cannot repair our accumulated errors, then we must experience an exponential death rate with its inevitable population crash, and none of us will live long with debility.
Either we will live into old age in good health...
...or we will live and die as we do today.